Code For 1
Hazrat Ali
Jon fought bravely to rescue the wildlings who were attacked by the white-walkers at Hardhome. On his arrival, Sam tells him that he wants to go to Oldtown to train at the Citadel to become a maester, so he can return and take the deceased Aemon's place as maester of Castle Black. Jon agrees to Sam's proposal and Sam sets off his journey to the Citadel. However becoming a trainee at the Citadel is not a cakewalk and hence the maesters at the Citadel gave Sam a problem to test his eligibility.
Initially Sam has a list with a single element n. Then he has to perform certain operations on this list. In each operation Sam must remove any element x, such that x > 1, from the list and insert at the same position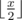 
, 
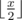, sequentially. He must continue with these operations until all the elements in the list are either 0 or 1.
Now the masters want the total number of 1s in the range l to r (1-indexed). Sam wants to become a maester but unfortunately he cannot solve this problem. Can you help Sam to pass the eligibility test?
The first line contains three integers n, l, r (0 ≤ n < 250, 0 ≤ r - l ≤ 105, r ≥ 1, l ≥ 1) – initial element and the range l to r.
It is guaranteed that r is not greater than the length of the final list.
Output the total number of 1s in the range l to r in the final sequence.
7 2 5
4
10 3 10
5
Solution
#include <bits/stdc++.h>
using namespace std;
int main()
{
long long n, l, r;
cin >> n >> l >> r;
l--, r--;
if (n == 0)
{
cout << 0 << endl;
}
else
{
set<long long> zeros;
long long nc = n;
for (int i = log2(nc); i > 0; i--)
{
long long sz = pow(2, i) - 1;
if (nc % 2 == 0)
{
zeros.insert(sz);
}
nc /= 2;
}
long long tmp = 0;
for (auto z: zeros)
{
long double d = 2 * (z + 1);
long long lower = ceil((l - z) / d);
long long upper = floor((r - z) / d);
tmp += upper - lower + 1;
}
cout << r - l + 1 - tmp << endl;
}
return 0;
}